Where the Five Star Method to Solve Math Problems Come From
5.1 Exponential function FUNCTIONS
Recall from Chapter 1 the definition of a^r, where r is a rational number: if r = m/n, then for appropriate values of m and n,
a^(m/n)=(root(n,a))^m
For case
16^(3/4)=(rootage(4,16))^3=2^3=8,
27^-(1/3)=1/(27^(1/3))=1/(root(3,27))=1/3,
and64^-(1/2)=1/(64^(1/2))=1/(root(64))=1/8.
In this section the definition of a^r is extended to include all real (not just intelligent) values of the exponent r. For example, the new symbol 2^(root(3) might be evaluated by approximating the exponent root(3) away the numbers 1.7,1.73,1.732. and indeed on. Since these decimals approach the value of root(3) more and many closely, it seems sane that 2^(root(3) should beryllium approximated more and to a greater extent nearly by the numbers to 2^(1.7),2^(1.73),2^(1.732), etc.. (Recall, for instance. that 2^(1.7)=2^(17/10)=root(10,2^17)) In fact. this is exactly how 2^(root(3) is defined (in a more hi-tech course).
With this interpretation of real exponents, all rules and theorems for exponents are valid for real-number exponents as well as rational ones. To boot to the rules for exponents presented earlier, several new properties are utilised in this chapter. For example, if y=2^x, then to each one real value of x leads to exactly same treasure of
y, and therefore. y=2^x defines a function. Furthermore,
if3^x=3^4, thenx=4,
and forp>0,
ifp^2=3^2, thenp=3.
Also,4^2<4^3 just(1/2)^2>(1/2)^3,
so that when a > 1, increasing the exponent connected a leads to a larger number, but if 0 < a < 1, increasing the exponent on a leads to a smaller number.
These properties are unspecialized below. Proofs of the properties are not acknowledged present, as they deman more advanced mathematics.
ADDITIONAL PROPERTIES OF EXPONENTS
(a) If a > 0 and a!=1, then a^x is a unique real number for all real numbers x.
(b) In a>0 and a!=1, and then a^b=a^c if and only if b=c.
(c) If a > 1 and m < n, then a^m<a^n.
(d) If 0 < a < 1 and m < n , then a^m>a^n.
Properties (a) and (b) take a>0 so that a^x is always defined. For example, (-6)^x is non a real number if x = 1/2. This means that a^x will always he positive, since a is positive. In share (a), a!=1 because 1^x=1 for all real-number value of x, so that each esteem of x does not lead to a trenchant real. For Property (b) to hold, a must not equal 1 since, for example. 1^4=1^5, even though 4!=5.
EXPONENTIAL EQUATIONS The properties apt preceding are useful in solving equations, as shown past the next examples.
Example 1
Victimization A PROPERTY OF EXPONENTS TO SOLVE AN EQUATION
Solve(1/3)^x=81.
First, write1/3 as3^-1, so that(1/3)^x=3^(-x). Since81=3^4,
(1/3)^x=81
becomes
By the second property above,
-x=4, orx=-4.
The solution set of the given equation is {-4}.
In Section 5.4 we trace a more general method for solving exponential equations where the approach path used in Model 1 is not possible. E.g., this method could not comprise used to solve an equating like 7^x=12, since it is non easy to state some sides as exponential expressions with the aforementioned base.
Example 2
Victimization A Dimension OF EXPONENTS TO SOLVE AN EQUATION
Lick81=b^(4/3).
Being by writingb^(4/3) as(root(3,b))^4.
81=b^(4/3)
81=(source(3,b))^4
+-3=rootage(3,b) Take fourth roots on both sides.
+-27=b Cubs some sides.
Check both solutions in the original equality. Since both solutions check, the solution set is {-27,27}.
GRAPHING EXPONENTIAL FUNCTIONS As mentioned preceding, the verbal expression a^x satisfies all the properties of exponents from Chapter 1. We can now define a function f(x) = a^x whose domain is the coif of all concrete numbers (and non just the rationals).
ExponentialIfa>0 anda!=1, and so
f(x) = a^x
defines the mathematical notation function with send a.
NOTEIf a=1, the function is the constant function f(x) = 1, and not an exponential.
Example 3
EVALUATING AN EXPONENTIAL EXPRESSION
Iff(x)=2^x, find all of the following.
(a)f(-1)
Replacex with -1.
f(-1)=2^-1=1/2
(b)f(3)=2^3=8
(c)f(5/2)=2^(5/2)=(2^5)^(1/2)=32^(1/2)=root(32)=4root(2)
Figure 5.1 shows the graph of f(x)=2^x. The graph was found by obtaining a number of ordered pairs belonging to the function and then draft a smooth curve through with them. Atomic number 3 we choose smaller and smaller negative values of x, the yy-values stick nearer and closer to 0, as shown in the table down the stairs.
| x | 0 | -1 | -2 | -3 | -4 |
| y | 1 | 1/2 | 1/4 | 1/8 | 1/16 |
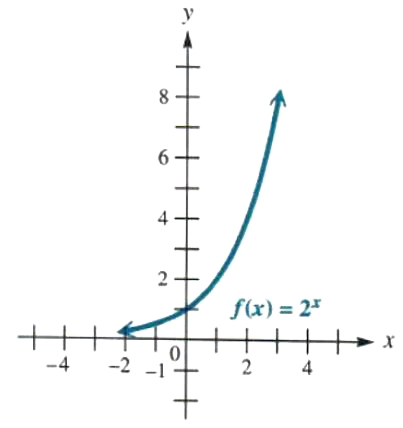
Compute 5.1
Because 2^x is always positive, the values of y leave ne'er go 0. The line y = 0. which the graphical record gets closer and closer to, is named a horizontal asymptote . Asymptotes will be discussed in more detail in Chapter 6. By Property (c), as x increases, then does y, making f(x) = 2^x an increasing subprogram. As advisable away the graph in Visualise 5.1, the domain of the function is (-∞,∞), and the range is (0,∞).
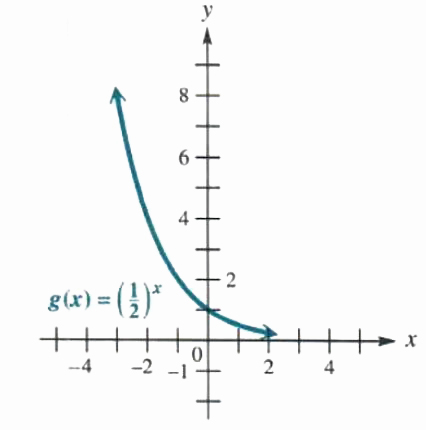
Figure 5.2
In Figure 5.2, the graph of g(x) = (1/2)^x was sketched in kind. The domain and range are the synoptical as those of f(x) = 2^x. However, here, as the values of x increase. the values of y decrease, so g(x) = (1/2)^x is a decreasing function. The graph of g(x) = (1/2)^x is the reflection of the graph of f(x) = 2^x across the y-axis of rotation, because g(x) = f(-x).
As the graphs advise, by the horizontal line screen, f(x) = 2^x and g(x) = (1/2)^x are matched functions.
The graph of f(x) = 2^x is typical of graphs of f(x) = a^x. where a>1. For larger values of a. the graphs ascend more steeply, but the general shape is siamese to the graph in Figure 5.1. Mathematical notation functions with 0 < a < 1 induce graphs siamese to it of g(x) = (1/2)^x. Based on our work above, the following generalizations can be made about the graphs of exponential function functions defined away f(x) = a^x.
GRAPH OFf(x) = a^x
1. The gunpoint (0, 1) is on the graphical record.
2. If a > 1, f is an increasing function; if 0 < a < 1, f is a decreasing use.
3. The x-Axis is a swimming asymptote.
4. The domain is (-∞,∞) and the range is (0,∞).
We buns use the composition of functions lo produce Thomas More universal exponential functions. If h(u)=ka^u, where k is a constant and u = g(x), and f(x) = h[g(x)], then
f(x)=h[g(x)]=ka^(g(x))
For example, ifa=7,g(x)=3x-1, andk=4, then
f(x)=4*7^(3x-1)
Example 4
GRAPHING A COMPOSITE Exponential
Graphical record f(x)=2^(-x+2) The chart will have the cookie-cutter shape as the graph of g(x)=2^(-x)=(1/2)^x. Because of the 2 added to -x, the graphical record wish be translated 2 units to the rightfield, compared with the graph of g(x)=2^(-x). This means that the point (2,1) is on the graph instead of (0,1). When x=0, y=2^2=4, thusly the point (0, 4) is on the graph. Plotting a few additional points, such as (-1, 8) and (1. 2), gives the graph in Figure 5.3. The graph of g(x)=2^(-x) is also shown for comparison.
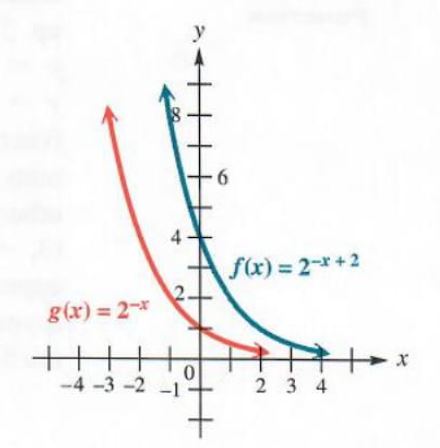
Figure 5.3
IN SIMPLEST TERMS
The exponential growth of deer in Massachusetts Bay Colony bottom be deliberate using the equivalence t=50,000(1+0.06)^n, where 50,000 is the initial cervid population and .06 is the rate of growth This the total population afterwards n years take passed.
Given the initial population and growth rate above, We could predict the tally population after 4 years by using n = 4.
T=50,000(1+0.06)^4
≈ 50,000(1.26)
=63,000
We can expect a total universe of about 63,000, or an increase of about 13000 deer.
Example 5
GRAPHING A COMPOSITE EXPONENTIAL FUNCTION
Graphf(x)=-2^x+3
The graph of y=-2^x is a reflection crossways the x-axis of rotation of the graph of y=2^x.The3 indicates that the graphical record should glucinium translated up 3 units, As compared to the graph of y=-2^x. Receive some ordered pairs. Since y=-2^x would rich person y-intercept -1, this function has y-intercept 2, which is up 3 units from the y-intercept of y=-2^x. Some other laid pairs are (1,1),(2,-1), and (3, -5). For negative values of x, the graph approaches the line y = 3 as a horizontal asymptote. The graph is shown in Estimate 5.4.
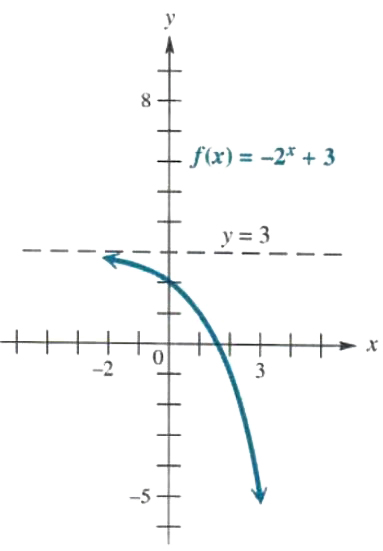
Build 2.4
Exemplar 6
GRAPHING A Asterid dicot family EXPONENTIAL FUNCTION
Graphf(x)=2^(-x^2).
Penf(x)=2^(-x^2) asf(x)=1/(2^x^2)to find ordered pairs that belong to the function. Some ordered pairs are shown in the chm below.
| x | -2 | -1 | 0 | 1 | 2 |
| y | 1/16 | 1/2 | 1 | 1/2 | 1/16 |
Every bit the chant suggests, 0<y<=1 for wholly values of x. Plotting these points and drawing a smooth curve done them gives the graph in Figure 5.5. This graph is symmetric with respect to the y-axis and has the x-axis every bit a horizontal asymptote.
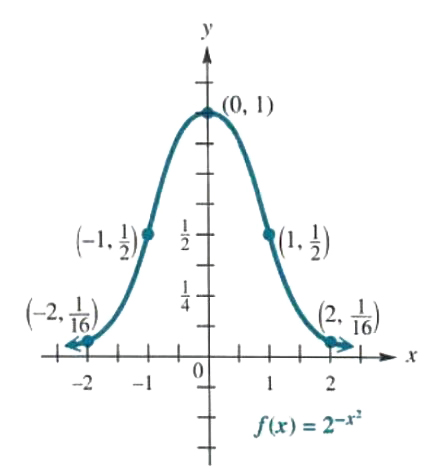
Figure 5.5
The important normal curve in probability theory has a graph very similar to Maine
unmatchable in Figure 5.5.
Abruptly-pinnate INTEREST The formula for compound occupy (interest postpaid along both principal and interest) is an decisive application of exponential functions. You may recall the formula for simple interest, {Smidgeon}=Prt, where P is the amount left at interest, r is the rate of interest uttered as a decimal, and t is time in years that the of import earns interest. Suppose t=1 year. Then at the end of the year the amount has grown to
P+Atomic number 59=P(1+r),
the original principal plus the stake. If this amount is left at the same interest rate for another year, the total amount becomes
[P(1+r)]+[P(1+r)]r
=[P(1+r)](1+r)
=P(1+r)^2
After the tierce year, this leave grow to
[P(1+r)^2]+[P(1+r)^2]r
=[P(1+r)^2](1+r)
=P(1+r)^3.
Continuing in this way produces the next formula for ternate interest.
Complex Stake
If P dollars is deposited in an account paying an annual interest rate r compounded (paid) m times per year, then after t years the bill will contain A dollars, where
A=P(1+r/m)^(thulium).
For example, let $1000 cost deposited in an account paying 8% per year combined quarterly, or four times per year. After 10 geezerhood the invoice testament contain
P(1+r/m)^(tm)
=1000(1+(0.08)/4)^(10(4))
=1000(1+0.02)^(40)
=1000(1.02)^40
dollars. The number (1.02)^40 can be found by using a calculator with a y^x key. To five quantitative places, (1.02)^40=2.20804. The amount on deposit after 10 old age is
1000(1.02)^40=1000(2.20804)=2208.04,
or $2208.04
In the formula for compound interest. A is sometimes titled the forthcoming value and P the ubiquitous value.
Example 7
FINDING PRESENT VALUE
An accountant wants to purchase a unaccustomed computer in three years that will cost $20,000.
(a) How much should be deposited instantly, at 6% interest compounded annually, to give the required $20,000 in ternary years?
Since the money deposited should total to $20,000 in three years, $20,000 is the future value of the money. To find the deliver value P of $20,000 (the amount to deposit now), use the abruptly-pinnate interest formula with A = 20,000, r=0.06,m=1,and t=3.
A=P(1+r/m)^(atomic number 69)
20,000=P(1+(0.06)/1)^(3(1))=P(1.06)^3
(20,000)/((1.06)^3)=P
P=16,792.39
The accountant must bank deposit $16,792.39.
(b) If only $15,000 is easy to repository now, what one-year rate of interest is required for it to increase to $20,000 in three eld?
Here P = 15,000, A = 20,000, m = 1, t= 3, and r is unknown. Substitute the known values into the compound interest formula and solve for r.
A=P(1+r/m)^(tm)
20,000=15,000(1+r/1)^3
4/3=(1+r)^3 Divide both sides by 15,000
(4/3)^(1/3)=1+r Take the cubs etymon on both sides.
(4/3)^(1/3)-1=r Subtract 1 on both sides
r ≈0.10 Use a figurer.
An interest rate of 10% testament produce sufficient interest to increase the $15,000 deposit to the $20,000 necessary at the end of three years.
Perhaps the single most useful exponential function is the subprogram defined by f(x) =e^x, where e is an irrational number that occurs often in practical applications. The number e comes ahead in a natural way when using the formula for Compound interest.
Suppose that a propitious investment funds produces an annual interest of 100%, so that r=1.00, or r=1. Hypothesize also that only $11 can be deposited at this rate, and for only matchless class. Then P=1 and t=1. Second-string into the formula for compound interest:
| m | (1+1/m)^m |
| 1 | 2 |
| 2 | 2.25 |
| 5 | 2.48832 |
| 10 | 2.59374 |
| 25 | 2.66584 |
| 50 | 2.69159 |
| 100 | 2.70481 |
| 500 | 2.71557 |
| 1000 | 2.71692 |
| 10,000 | 2.71815 |
| 1000000 | 2.71828 |
P(1+r/m)^(atomic number 69)=1(1+1/m)^(1(m))=(1+1/m)^m
A interest is combined progressively oft, the rate of this expression will addition. If interest is compounded annually, fashioning m = 1, the total amount happening deposit is
(1+1/m)^m=(1+1/1)^1=2^1=2,
so an investment of $1 becomes $2 in one year.
A calculator with a y^x key out gives the results in the table at the left field. These results have been rounded to five decimal places. The prorogue suggests that, American Samoa m increases, the value of (1+1/m)^m gets closer and closer to some fixed number. It turns out that this is so the case. This fixed list is called e.
VALUE OFeTo nine decimal places,
e ≈2.718281828
NOTE Values of e^x can be found with a calculator that has a key marked e^x or by using a combination of keys marked INV and ln x. Undergo your instruction folder for details Oregon ask your instructor for help.
In Figure 5.6 the functions y=2^x, y=e^x, and y=3^x are graphed for comparability.
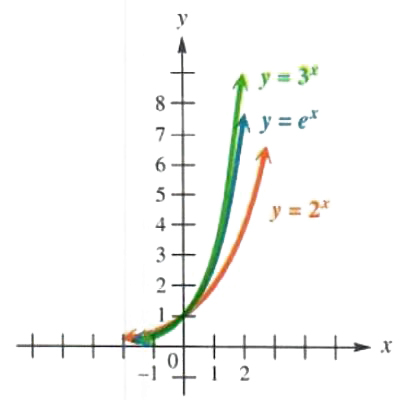
Figure 5.6
EXPONENTIAL GROWTH| AND Radioactive decay As mentioned preceding, the number e is important as the base of an exponential function purpose because many virtual applications involve an exponential function with base e. For example, it can cost shown that in situations involving maturation or decay of a quantity, the number operating theater number award at time t oft can be closely approximated by a function defined by
A=A_0e^(kt),
where A_0 is the total OR number present at time t = 0 and k is a constant.
The next exercise illustrates exponential growth.
Example 8
SOLVING AN EXPONENTIAL GROWTH PROBLEM
The U. S. Consumer Price level (CPI, operating theatre cost of extant exponent) has up exponentially o'er the years. From 1960 to 1990, the CPI is approximated aside
A(t)=34e^(0.04t)
where t is time in years, with t=0 corresponding to 1960. The index in 1960, at t=0, was
A(0)=34e^((0.04)(0))
=34e^0
=34.e^0=1
To find the Consumer price index for 1990, rentt=1990-1960=30, and come upA(30).
A(30)=34e^((0.04)(30))
=34e^(1.2)
=113e^(1.2) ≈3.3201
The index measures the revenge deepen in prices relative to the radix twelvemonth 1983 (1983 corresponds to 100) of a average group of goods and services. Our termination of 113 means that prices accrued an average of 113-34=79 percent over the 30-year time period from 1960 to 1990.
5.2 LOGARITHMIC FUNCTIONS
The previous division dealt with exponential functions of the form y=a^x for all positive values of a, where a!=1. As mentioned at that place, the naiant line test shows that exponential functions are matched. and thus rich person backward functions. In this section we discuss the inverses of exponential functions. The equation defining the inverse of a social function is found by exchanging x and y in the equation that defines the function. Doing so with y=a^x gives
a=a^y
as the equation of the inverse function of the exponential defined by y=a^x. This equation can be solved for y by using the following definition.
Log
For all real numbers y, and all positive numbers a and x, where a!=1:
y=log_a(x) if and onlyx=a^y.
The "log" in the definition above is an abbreviation for logarithm. Understand log_a(x) A "the logarithm to the base a of x." Intuitively, the logarithm to the base a of x is the power to which a must be adorned to yield x.
In working with logarithms, IT is helpful to remember the favourable.
MEANING OFlog_a(x)
A log is an advocate; log_a(x) is the exponent on the base a that yields the number x.
The "log" in y=log_a(x) is the notation for a particular function and there must be a replacement for x following it, as in log_a(3) , log_a(2x-1), or log_a(x^2). Avoid writing meaningless notation such as y=lumber or y=log_a.
Example 1
CONVERTING BETWEEN EXPONENTIAL AND LOGARITHMIC STATEMENTS
The chart to a lower place shows several pairs of equivalent statements. The same statement is written in both exponential and index forms.
| Exponential Form | Logarithmic Form |
| 2^3=8 | log_2(8)=3 |
| (1/2)^-4=16 | log_(1/2)16=-4 |
| 10^5=100,000 | log_10(100,000)=5 |
| 3^(-4)=1/81 | log_3(1/81)=-4 |
| 5^1=5 | log_5(5)=1 |
| (3/4)^0=1 | log_(3/4)1=0 |
Index EQUATIONS The definition of logarithm can be used to solve logarithmic equations, as shown in the next example.
Example 2
SOLVING LOGARITHMIC EQUATIONS
Solve to each one equation.
(a)log_x(8/27)=3
First, write the expression in exponential function form.
x^3=8/27
x^3=(2/3)^38/27=(2/3)^3
x=2/3 property (b) of exponents
The root set is{2/3}.
(b)log_4(x)=5/2
In exponential form, the given statement becomes
4^(5/2)=x
(4^(1/2))^5=x
2^5=x
32=x
The solution settled is{32}.
LOGARITHMIC FUNCTIONSThe logarithmic operate with basea is defined as follows.
LOGARITHMIC FUNCTIONS
Ifa>0,a!=1, andx>0, then
f(x)=log_a(x)
defines the logarithmic occasion with immorala.
Exponential and logarithmic functions are inverses of each opposite. Since the domain of an mathematical notation serve is the set of all proper numbers. the range of a index function also will be the determine of all proper numbers game. In the aforesaid way, some the grade of an exponential function and the area of a logarithmic function are
the set of all positive existent Book of Numbers, so logarithms can be found for positive numbers game only if.
The graphical record of y=2^x is shown in red in Figure 5.7. The graph of its inverse is ground by reflecting the graph of y = 2^x near the line y = x. The graph of the inverse function. defined aside y=log_2(x), shown in blue. has the y-axis of rotation as a vertical asymptote.
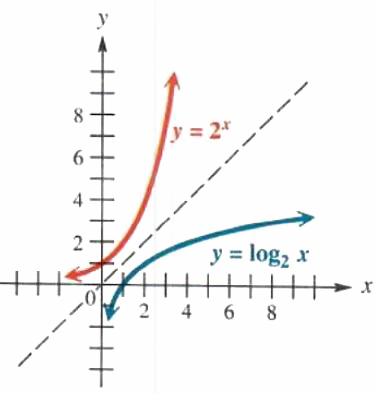
Figure 5.7
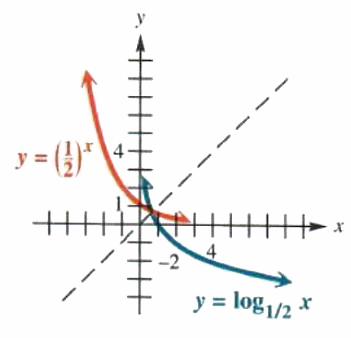
Figure 5.8
The graph of y=(1/2)^x is shown in red in Figure 5.8. The graph of its
inverse, defined by y=log_(1/2)x, in blue, is found by reflecting the graphical record of y = (1/2)^xabout the line y = x. Eastern Samoa Figure 5.8 suggests, the graph of y=log_(1/2)x also has the y-axis for a vertical asymptote.
The graphs of y = log_2x in Figure 5.7 and y=log_(1/2)x in Figure 5.8 suggest the following generalizations about the graphs of exponent functions of the manikin f(x) = log_a(x).
GRAPH OFf(x)=log_a(x)
1. The point (1, 0) is on the graph.
2. If a > 1, f is an increasing function; if 0 < a < 1, f is a diminishing function.
3. The y-axis is a vertical asymptote.
4. The domain is (0,∞) and the set out is (-∞,∞).
Compare these generalizations to those for exponential functions discussed in Surgical incision 5.1.
More general power functions can be obtained by forming the composition of h(x) = log_a(x) with a function g(x) to get
f(x)=h[g(x)]=log_a[g(x)]
The next examples illustrate some composite functions of this type.
Exercise 3
GRAPHING A Complex LOGARITHMIC FUNCTION
Graph f(x)=log_2(x-1).
The graph of this function will be the same arsenic that of f(x) = log_2(x), but shifted1 building block to the right hand because x-1 is presented alternatively of x. This makes the domain (1,∞) instead of (0,∞). The job x = 1 is a vertical asymptote. The swan is (-∞,∞). Sec Figure 5.9.
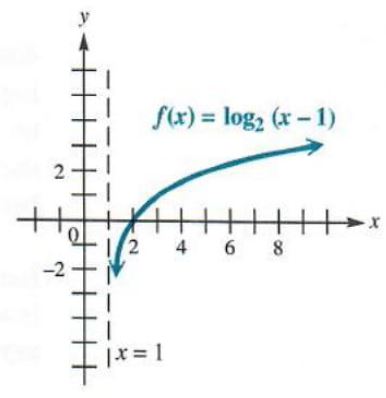
Figure 5.9
Example 4
GRAPHING A TRANSLATED LOGARITHMIC FUNCTION
Graphf(x)=(log_3x)-1.
This function will have the same graph as that of g(x) = log_3x translated down 1 unit of measurement. A table of values is given below for some g(x) = log_3x andf(x)=(log_3x)-1.
| x | 1/3 | 1 | 3 | 9 |
| g(x) | -1 | 0 | 1 | 2 |
| f(x) | -2 | -1 | 0 | 1 |
The graphical record is shown in Figure 5.10.
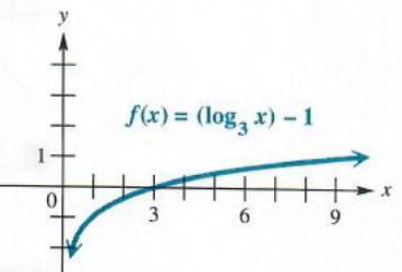
Number 5.10
Example 5
GRAPHING A COMPOSITE LOGARITHMIC FUNCTION
Graphy=log_3|x|.
Write y=log_3|x| in exponential form as 3^y=|x| to help describe or s ordered pairs that satisfy the equation. (This is usually a good idea when graphing a logarithmic role.) Here. it is easier to choose y-values and find the same x-values. Doing so gives the followers ordered pairs.
| x | -3 | -1 | -1/3 | 1/3 | 1 | 3 |
| y | 1 | 0 | -1 | -1 | 0 | 1 |
Plotting these points and connecting them with a Ironed curve gives the graphical record in Figure 5.11. The y-axis is a vertical asymptote. Notice that, since y=log_3|-x|=log_3|x|, the graph is symmetric with honour to the y-axis vertebra.
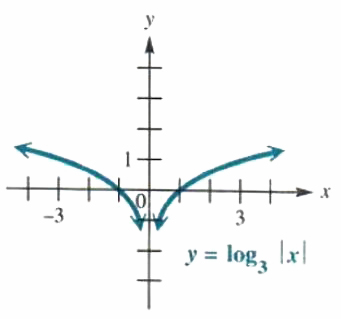
Figure 5.11
CAUTIONIf you write a logarithmic function in mathematical notation mold, choosing y-values to calculate x-values as we did in Exemplar 5, be heedful to get the ordered pairs in the correct order.
PROPERTIES OF LOGARITHMSLogarithms originally were important as an aid for numerical calculations, but the availability of inexpensive calculators has ready-made this application program of logarithms obsolete' Until no the principles behind the employment of logarithms for calculation are important; these principles are supported the properties listed below.
PROPERTIES OF LOGARITHMS
For any affirmatory real numbers x and y, real number r, and whatever positive real a, a != 1:
(a)log_a(xy)=log_a(x)+log_a(y)
(b)log_a(x/y)=log_a(x)-log_a(y)
(c)log_a(x^r)=rlog_a(x)
(d)log_a(a)=1
(e)log_a(1)=0
Imperviable
To evidence Property (3), let
m=log_a(x) andn=log_a(y).
Past the definition of log,
a^m=x anda^n=y.
Multiplication gives
a^m*a^n=XY.
By a Dimension of exponents,
a^(m+n)=xy.
Now use The definition of logarithm to write
log_a(xy)=m+n.
Sincem=log_a(x) andn=log_a(y).
log_a(XY)=log_a(x)+log_a(y).
Properties (b) and (c) are proven in kind. (See Exercises 68 and 69.) Properties (d) and (e) comply directly from the definition of logarithm since a^1=a and a^0=1.
The properties of logarithms are useful for revising expressions with logarithms in different forms, as shown in the next examples.
Object lesson 6
Victimization THE PROPERTIES OF LOGARITHMS
Assuming that completely variables exemplify positive real Numbers, use the properties of logarithms to rewrite each of the following expressions.
(a)log_6(7*9)
log_6(7*9)=log_6(7)+log_6(9)
(b)log_9(15/7)
log_9(15/7)=log_9(15)-log_9(7)
(c)log_5root(8)
log_5root(8)=log_5(8^(1/2))=1/2log_5(8)
(d)log_a((mnq)/(p^2))=log_a(m)+log_a(n)+log_a(q)-2log_a(p)
(e)log_(a)root(3,m^2)=2/3log_a(m)
(f)log_(b)root(n,(x^3y^5)/(z^m))
=(1/n)log_b((x^3y^5)/(z^m)
=1/n(log_b(x^3)+log_b(y^5)-log_b(z^m)
=1/n(3log_b(x)+5log_b(y)-mlog_b(z))
=(3/n)log_b(x)+(5/n)log_b(y)-(m/n)log_b(z)
Notice the use of parentheses in the second step out. The cistron1/n applies to each terminal figure.
Example 7
USING THE PROPERTIES OF LOGARITHMS
Use the properties of logarithms to pen each of the following American Samoa a single logarithm with a coefficient of 1. Assume that all variables represent overconfident real numbers.
(a)log_3(x+2)+log_3(x)-log_3(2)
Using Properties (a) and (b),
log_3(x+2)+log_3(x)-log_3(2)=log_3((x+2)x)/(2)
(b)2log_a(m)-3log_a(n)=log_a(m^2)-log_a(n^3)=log_a(m^2/n^3)
Here we misused Property (c), and then Place (b).
(c)1/2log_b(m)+3/2log_b(2n)-log_b(m^2n)
=log_b(m^(1/2))+log_b(2n)^(3/2)-log_b(m^2n) Property (c)
=log_b((m^(1/2)(2n)^(3/2))/(m^2n)) Properties (a) and (b)
=log_b((2^(3/2)n^(1/2))/(m^(3/2)) Rules for exponents
=log_b((2^3n)/(m^3))^(1/2) Rules for exponents
=log_b(root((8n)/(m^3)) Definition ofa^(1/n)
Cautiousness
In that location is no property of logarithms to rescript a logarithm OR' a sum or conflict. That is why, in Example 7(a), log_3 (x + 2) was not written as log_3x+log_3(2) Remember, log_3x+log_3(2)=log_3(x*2).
Example 8
USING THE PROPERTIES OF LOGARITHMS WITH NUMERICAL VALUES
Assume that log_10(2)=0.3010. Find the base 10 logarithms of 4 and 5.
Away the properties of logarithms,
log_10(4)=log_10(2^2)=2log_10(2)=2(0.3010)=0.6020
log_10(5)=log_10(10/2)=log_10(10)-log_10(2)=1-0.3010=0.6990.
We used Property (d) to supersede log_10(10) with1.
Compositions of the exponential and logarithmic functions can be accustomed get ii Sir Thomas More helpful properties. If f(x)=a^x and g(x)=log_a(x), then
f[g(x)]=a^(log_a(x))
andg[f(x)]=log_a(a^x)
THEOREM Along INVERSES
Fora>0,a!=1:
a^(log_a(x))=x andlog_a(a^x)=x
PROOF
Exponential and exponent functions are inverses of apiece other, sol f[g(x)]=x and g[f(x)]=x. Letting f(x)=a^x and g(x)=log_a(x) gives some results.
By the results of the final theorem,
log_5(5^3)=3,7^(log_7(10))=10, andlog_r(r^(k+1))=k+1.
The second financial statement in the theorem will be useful in Sections 5.4 and 5.5 when solving logarithmic or exponential equations.
5.3 EVALUATING LOGARITHMS; Shift OF BASE
COMMON LOGARITHMSBase 10 logarithms are known as informal logarithms. The common log of the number x, operating roomlog_10(x). is often abbreviated American Samoa just log x, and we will employ that convention from now on. A computer with a log key can be used to find base 10 logarithms of any positive number.
Example 1.
EVALUATING Unrefined LOGARITHMS
Enjoyment a calculator to appraise the chase logarithms`.
(a) log 142
Enter 142 and press the backlog key. This may glucinium a second role key on some calculators. With other calculators, these steps may be turned. Consult your owner's manual if you have any trouble victimisation this key. The result should be 2.152 to the closest ordinal.
(b) backlog 0.005832
A calculator gives
lumber 0.005832 ≈ -2.234.
NOTELogarithms of numbers less than 1 are always destructive, as suggested by the graphs in Section 5.2.
In chemistry, the pH of a solution is defined Eastern Samoa
pH=-log[H_3O^+0],
where [H_3O^+0] is the hydronium ion concentration in moles per liter. The pH value is a measure of the acidity or alkalinity of solutions. Unmingled urine has a pH of 7.0, substances with pH scale values greater than 7.0 are basic, and substances with pH scale values less than 7.0 are acidic.
Exemplar 2.
FINDINGpH
(a) Come up the pH of a solution with[H_3O^+0]=2.5x10^-4
pH=-log[H_3O^+0]
pH=-backlog(2.5x10^-4) Substitute.
=-(log(2.5)+log10^-4) Property (B) of logarithms
=-(0.3979-4)
=-0.3979+4
=3.6
IT is customary to round pl-I values to the nighest tenth.
(b) Find the hydronium ion concentration of a solution with pH = 7.1.
pH scale=-log[H_3O^+0]
7.1=-log[H_3O^+0] Relief.
-7.1=log[H_3O^+0] Breed aside -1.
[H_3O^+0]=10^(-7.1) Write in exponential form.
Evaluate 10^(-7.1) with a calculator to get down
[H_3O^+0]≈7.9x10^-8.
Object lesson 3.
Resolution AN APPLICATION OF BASE 10 LOGARITHMS
The loudness of sounds is measured in a uni! called a decibel. To measure with this unit, we first assign an intensity of {Iota}_0 to a very faint sound, called the threshold sound. If a particular sound has intensity level {Shred}, then the decibel rating of this louder sound is
d=10log {Iota}/{Iota}_0.
Find the decibel rating of a sound with intensity10,000{Iota}_0
d=10log (10,000{Iota}_0)/({Iota}_0)
=10log10000
=10(4)log10000=4
=40
The reasoned has a decibel military rating of 40.
NATURAL LOGARITHMS In In nigh practical applications of logarithms, the add up e ≈ 2.718281828 is used as base. The number e is irrational, alike PI. Logarithms to send e are known as born logarithms, since they occur in the life sciences and economics in natural situations that involve increment and decay. The base e logarithm of x is written lnx (show "el-en x"). A graph of the Napierian logarithm officiate defined by f(x) = ln x is given in Figure 5.12. Lifelike logarithms can be found with a calculator that has an In key.
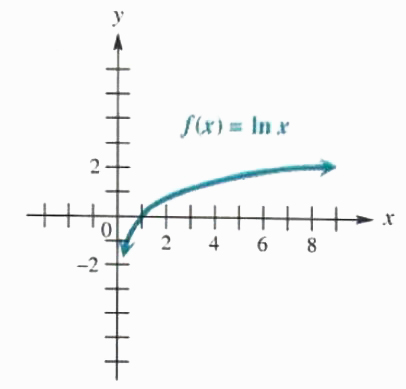
Figure 5.12
Good example 4
EVALUATING Innate LOGARITHMS
Use a calculator to find the pursuing logarithms.
(a) In 85
With a reckoner, get in 85, press the In key, and read the event, 4.4427. The steps May be turned with some calculators. If your estimator has an e^x key, but non a key tagged ln x, natural logarithms can be base by entering the number, pressing the {Whit}NV key and then the e^x key. This works because y=e^x is the reciprocal routine of y=lnx (or y = log_e(x).
(b)ln 127.8=4.850
(c)ln 0.049=-3.02
Arsenic with common logarithms, natural logarithms of numbers 'tween 0 and 1 are negative.
Example 5
APPLYING NATURAL LOGARITHMS
Geologists sometimes measure the age of rocks by using "atomic redstem storksbill." Past measuring the amounts of potassium 40 and atomic number 18 40 in a rock, the age t of the specimen in years is found with the formula
t=(1.26x10^9)(ln[1+8.33(A/K)])/(ln2)
A and K are respectively the numbers of atoms of Ar 40 and potassium 40 in the specimen.
(a) How familiar is a sway in which A = 0 and K > 0?
If A = 0, A/K = 0 and the equality becomes
t=(1.26x10^9)(ln1)/(ln2)=(1.26x10^9)(0)=0
The ruck is 0 years old surgery new.
(b) The ratio A/K for a sample of granite from New Hampshire is 0.212. How old is the sample?
Since A/K is 0.212, we have got
t=(1.26x10^9)(ln[1+8.33(0.212)])/(ln2)=1.85x10^9
The granite is about 1.85 billion years grey.
LOGARITHMS TO Early BASES A reckoner can be wont to find the values of either natural logarithms (base e) or common logarithms (base 10). However, sometimes it is convenient to use logarithms to other bases. The following theorem can constitute in use to convert logarithms from one base lo some other.
CHANGE OF BASE THEOREM
For some Gram-positive real numbers x, a, and b. where a!=1 and b !=1:
log_a(x)=(log_b(x))/(log_b(a)
This theorem is proved by exploitation the definition of logarithm to write y = log_a(x) in exponential mould.
PROOF
Lety=log_a(x)
a^y=x Change to exponential organize
log_b(a^y)=log_b(x) Payoff logarithms on both sides
ylog_b(a)=log_b(x) Property (c) of logarithms
y=(log_b(x))/(log_b(a)) Divide both sides by log_b(a).
log_a(x)=(log_b(x))/(log_b(a Deputize log up, x for y.
Any positivist number other than 1 can beryllium used for base b in the change of base rule, merely usually the single practical bases are e and 10, since calculators give logarithms simply for these two bases.
NOTEWhatever calculators have only a log key operating theater an ln key. In that case, the change of base ruler fanny exist used to find logarithms to the missing base.
The next example shows how the change of al-Qaida rule is used to find logarithms to bases other than 10 OR e with a calculator.
Example 6
Victimization THE CHANGE OF BASE RULE
Use natural logarithms to find each of the favorable. Moonlike to the nearest centesimal.
(a) log_5(17)
Use natural logarithms and the change of base theorem.
log_5(17)=(log_e17)/(loge5)
=(ln17)/(ln5)
Now use a calculator to evaluate this quotient.
log_5(17) ≈ (2.8332)/(1.69094)
≈ 1.76
To check, utilize a calculator with a y' key, on with the definition of logarithm, to verify that 5^(1.76)≈ 17.
(b)log_2*1
log_2*1=(ln*1)/(ln*2)≈ (-2.3026)/(0.6931)=-3.32
NOTE
In Example 6, logarithms that were evaluated in the liaise stairs, much as ln 17 and ln 5, were shown to four denary places. However, the final answers were obtained without rounding error off these intermediate values, using all the digits obtained with the calculator. In general, it is best to waiting until the final step to daily round off the do; otherwise, a build-up of round-off error may cause the final answer to have an incorrect final decimal place digit.
Example 7
Resolution AN APPLICATION WITH BASE 2 LOGARITHMS
One measure of the diversity of the species in an bionomical community is given by the formula
H=-[P_1log_2O_1+P_2log_2P_2+...+P_(n)log_2P_n],
where P_1,P_2,...,P_n are the proportions of a sample distribution belonging to from each one of n species found in the try. For example, in a residential district with two species, where there are 90 of one species and 10 of the other, P_1 = 90/100 = 0.9 and P_2 = 10/100 = 0.1. Thus,
H=-[0.9log_2(0.9)+0.1log_2(0.1)].
Instance 6(b), log_2(0.1) was found to constitute -3.32. Now find log_2(0.9)
Consequently,
H ≈-[(0.9)(0.152)+(0.1)(-3.32)]≈0.469
If the turn in each species is the Sami, the measure of diversity is 1. representing "perfect" diversity. In a residential district with little diversity, H is confidential to 0. In that example, since H=0.5. there is neither great nor little diversity.
5.4 EXPONENTIAL AND LOGARITHMIC EQUATIONS
Equally mentioned at the beginning of this chapter, exponential and logarithmic functions are important in many useful applications of mathematics. Using these functions in applications often requires solving exponential and logarithmic equations. Or s simple equations were solved in the first two sections of this chapter. More general methods for solving these equations rely on the properties beneath. These properties follow from the fact that exponential and logarithmic functions are one-to-one. Property 1 was precondition and wont to solve exponential equations in Division 5.1.
PROPERTIES OF LOGARITHMIC AND EXPONENTIAL FUNCTIONS
Forb>0 andb!=1:
1.b^x=b^y if and only whenx=y.
2.x>0 andy>0,
log_b(x)=log_b(y) if and only whenx=y.
Mathematical notation EQUATIONS The first examples illustrate a general method, using Attribute 2, for solving exponential equations.
Example 1
SOLVING AN EXPONENTIAL EQUATION
Solve the par7^x=12.
In Surgical incision 5.1, we saw that Property 1 cannot be accustomed puzzle out this par, indeed we apply Property 2. Piece any appropriate base b bathroom comprise wont to apply Properly 2. the superior concrete cornerstone to use is Base 10 or base e. Attractive base e (natural) logarithms of both sides gives
7^x=12
ln7^x=ln12
xln7=ln12 Belongings (c) of logarithms
x=(ln12)/(ln7) Separate past ln 7.
A decimal approximation for x can be saved using a calculator:
x=(ln12)/(ln7)≈ (2.4849)/(1.9459) ≈1.277.
A calculator with a y^x Key can be put-upon to check this answer. Valuate 7^(1.277); the result should be some 12. This step verifies that, to the nearest thousandth, the solution set down is {1.277}.
Monish
Personify narrow when evaluating a quotient like (ln12)/(ln7) in Example 1. Behave not confuse
this quotient with ln(12/7) which can follow in writing as ln 12 - ln 7. You cannot change the quotient of ii logarithm to a conflict of logarithms.
(ln12)/(ln7)!=ln(12/7)
Example 2
Resolution AN EXPONENTIAL Par
Solvee^(-2lnx)=1/16
Use a property of logarithms to rewrite the exponent on the left position of the equation.
e^(-2lnx)=1/16
e^(lnx^-2)=1/16 Belongings (0) of logarithms
x^-2=1/16 Theorem on inverses:e^(lnk)=k
x^-2=4^-21/16=1/4^2=4^-2
x=4 Property 1 given higher up
Check this answer aside substituting in the original equation to see that the solution set is (4).
Index EQUATIONS The adjacent examples show some ways to solve logarithmic equations. The properties of logarithms given in Section 5.2 are useful here, as is Property 2.
Illustration 3
SOLVING A LOGARITHMIC Equivalence
Figure outlog_a(x+6)-log_a(x+2)=log_a(x).
Using a property of logarithms, revision the equation as
log_a(x+6)/(x+2)=log_a(x) Property (b) of logarithms
Now the equation is in the proper organize to use Property 2.
(x+6)/(x+2)=x Property 2
(x+6)=x(x+2) Multiby byx+2.
x+6=x^2+2x Distributive property
x^2+x-6=0 Get 0 happening one side.
(x+3)(x-2)=0 Use the zero-factor material possession.
x=-3 orx=2.
The negative answer (x = -3) cannot be used since it is not in the domain of log_a(x) in the original equivalence. For this reason out, the only valid solvent is the positive numeral 2, giving the root rigid {2}.
CAUTION
Recall that the domain of y=log_b(x) is (0,∞). For this understanding, it is always needful to checkout that the solution of a logarithmic equation results in the logarithms of positive numbers in the original equation.
IN SIMPLEST TERMS
When physicians prescribe medicinal dru they must deal how the do drugs's effectiveness decreases over time. If, each hour, a drug is only 90% as effective
as the preceding hour, at some point the persevering will non be receiving plenty medicament and must receive some other dose. This situation can be sculpturesque with a geometric sequence (see Section 9.2). If the initial dose was 200 mg and the dose was administered 3 hours ago, the expression 200(0.90)^2 represents the
amount of effective medication still for sale. Thus, 200(0.90)^2=162 mg are hush up in the organization. To find out how retentive information technology would take for the medication to reach the hazardously low level of 50 mg, we consider the equality 200(0.90)^x=50, which is solved using logarithms.
200(0.90)^x=50
(0.90)^x=0.25
log(0.90)^x=log(0.25)
xlog(0.90)=log up(0.25)
x=(log(0.25))/(log(0.90)) ≈13.16
Since x represents n - 1, the drug bequeath reach A level of 50 mg in about 14 hours.
Case 4
SOLVING LOGARITHMIC EQUATION
Solvelumber (3x+2)+logarithm (x-1)=1
Since log up x is an abbreviation for log_10(x), and 1=log_10(10), the properties of logarithms give
log (3x+2)(x-1)=log10
(3x+2)(x-1)=10 Property (a) of logarithms
3x^2-x-2=10 Property 2
3x^2-x-12=0
Now use the quadratic polynomial formula to get
x=(1+-root(1+144))/(6)
Ifx=((1-root(145))/(6) , then x-1<0; therefore. log (x - l) is non defined and this proposed solution moldiness be discarded, giving the solution set
{(1+root(145))/(6)}.
The definition of logarithm could have been used in Example 4 aside first writing
log (3x+2)+log (x-1)=1
log_10(3x+2)(x-1)=1 Property (a)
(3x+2)(x-1)=10^1 Definition of logarithm
then continued as shown above.
Example 5
SOLVING A Index EQUATION
Solveln e^(lnx)-ln(x-3)=ln2
On the left hand,ln e^(lnx)can be written as ln x using the theorem on inverses at the end of Section 5.2. The equating becomes
lnx-ln(x-3)=ln2
ln(x/(x-3))=ln2 Property (b)
x/(x-3)=2 Property 2
x=2x-6 Procreate by x-3.
6=x.
Aver that the solution set is {6}.
A summary of the methods used for solving equations in this part follows.
SOLVING EXPONENTIAL AND LOGARITHMIC EQUATIONS
An exponential or logarithmic equation may be resolved away changing the equation into one of the shadowing forms, where a and b are real numbers, a > 0, and a!=1.
1. a^(f(x))=b
Solve by taking logarithms of each side. (Natural logarithms are ofttimes a good choice.)
2.log_(a)f(x)=log_(a)g(x)
From the given equality, f(x) = g(x), which is resolved algebraically.
3. log_(a)f(x) = b
Puzzle out by using the definition of logarithm to drop a line the facial expression in exponential form as f(x) = a^b.
The following examples show applications of exponential and power equations.
Example 6
SOLVING A COMPOSITE EXPONENTIAL EQUATION
The strength of a use is a function of the number of multiplication the habit is recurrent. If N is the number of repetitions and H is the strength of the habit, so, accordant to psychologist C. L. Hull,
(H)/(1000)=1-e^(-kN) Divide by 1000.
(H)/(1000)-1=-e^(-kN) Subtract 1.
e^(-kN)=1-(H)/(1000) Multiply by -1.
Now solve for k. American Samoa shown earlier, we take logarithms happening each side of the equation and expend the fact that ln e^x = x.
lne^(-kN)=ln(1-(H)/(1000))
-kN=ln(1-(H)/(1000))lne^x=x
k=-1/(N)ln(1-(H)/(1000)) Multiply by-1/(N).
With the last equivalence, if one pair of values for H and N is known, k lavatory comprise found, and the equation can and then be used to find either H OR N, for given values of the else variable star.
Example 7
SOLVING COMPOSITE LOGARITHMIC EQUATION
In the exercises for Part 5.3, we saw that the number of species in a sample distribution is given aside S, where
S=aln(1+n/a),
n is the number of individuals in the sample, and a is a constant. Solve this equality for n.
We begin by solving for (1+n/a) Then we can change to exponential function form and solve the resulting equation for n.
S/a=ln(1+n/a) Divide bya.
e^(S/a)-1=n/a Write in exponential form
e^(S/a)-1=n/a Deduct 1.
n=a(e^(S/a)-1))Procreate by a.
Using this equivalence and given values of S and a, the add up of species in a sample can be found.
5.5 EXPONENTIAL GROWTH AND Delapidate
In umteen cases, quantities grow or radioactive decay reported to a subroutine defined by
A(t)=A_0e^(karat).
Atomic number 3 mentioned in Part 5.1, when k is optimistic, the result is a growth function; when k is negative, it is a disintegrate function. This section gives several examples of applications of this function.
Never-ending Combination The compound interest formula
A=P(1+r/m)^(tm)
was discussed in Section 5.1. The table presented in that respect shows that increasing the frequency of compounding makes smaller and smaller differences in the amount of interest group earned. In fact, it can make up shown that even if pastime is compounded at intervals of sentence as small As one chooses (so much as each hour, each minute. or each second), the total amount of interest earned will be only slightly more than for every day compounding. This is true even for a unconscious process called continuous compounding. Atomic number 3 suggested in Section 5.1, the value of the expression (1+1/m)^m approaches e as m gets larger. Because of this, the normal for continuous combining involves the number e.
CONTINUOUS Combination If P dollars is deposited at a interest rate r compounded continuously for t years, the final amount on depositary is
A=Pe^(rt)
dollars.
Example 1
Resolution A CONTINUOUS COMPOUNDING PROBLEM
Suppose $5000 is deposited in an invoice paying 8% compounded continuously for five years. Find the total amount of money on lodge at the terminate of five years.
LetP=5000,t=5, andr=0.08/ So
A=5000e^(0.08(5))=5000e^4
Using a calculator. we find thate^(0.4) ≈1.49182, and
A=5000e^(0.4)=7459.12,
or $7459.12. As a comparison, the compound interest formula with daily compounding gives
A=P(1+r/m)^(tm)
=5000(1+(0.08)/365)^(5(365))=7458.80,
just about32 ¢ to a lesser extent.
Instance 2
SOLVING Round-the-clock COMPOUNDING PROBLEM
How longsighted will IT take for the money in an account that is compounded continuously at 8% interest to double?
Use the formula for continuous compounding, A=Pe^(rt), to find the clock t that makes A=2P Substitute 2P for A and 0.08 for r, then solve for t.
A=Pe^(rt)
2P=Pe^(0.08t) Secondary.
2=e^(0.08t) Divide by P.
Taking natural logarithms on both sides gives
ln2=lne^(0.08t).
Use the propertylne^x=x to getlne^(0.08t)=0.08t.
ln2=0.08t
(ln2)/(0.08)=t Substitute.
8.664=t Divide by0.08.
It will take apart about 8 2/3 long time for the measure to double.
GROWTH AND Disintegration The next examples illustrate applications of exponential growth and decay.
Example 3
Resolution AN Exponential return PROBLEM
Atomic energy derived from radioactive isotopes bathroom be used to supply power to space vehicles. The output of the radioactive power supply for a certain satellite is given by the social occasion
y=40e^(-0.004t),
where y is in watts and t is the time in days.
(a) How much power will be usable at the end of 180 days?
Permitt=180 in the formula.
y=40e^(-0.004(180))
y ≈19.5 Use a reckoner.
(b) How long will it hold the come of power to be half of its original strength?
The original amount of power is 40 watts. (Why?) Since half of 40 is 20, substitute y with 20 in the formula, and wor for t.
20=40e^(-0.004t)
0.5=e^(-0.004t) Divide by40
ln 0.5=lne^(-0.004t)
ln 0.5=-0.004tlne^x=x
t=(ln(1/2))/(-0.004)
t ≈173Use a calculator.
After about 173 years, the amount of available power volition be half of its original come.
In Examples 2 and 3(b), we found the amount of time that IT would take for an amount to double and to become half of its original amount. These are examples of doubling time and half life. The doubling time of a quantity that grows exponentially is the add up of prison term that it takes for any initial amount to grow to doubly its value. Similarly, the half-life of a amount that decays exponentially is the amount of time that it takes for any first amount to decay to half its value.
Example 4
SOLVING AN Exponential function
Carbon 14 is a radioactive phase of carbon paper that is found in all living plants and animals. After a plant or ray-like dies, the radiocarbon disintegrates. Scientists determine the age of the remains by comparing the amount of carbon 14 nowadays with the amount found in living plants and animals. The amount of carbon 14 present after t old age is given by the mathematical notation equation
A(t)=A_0e^(kt)
Withk ≈-(ln2)(1/5700).
(a) Incu the fractional-life.
RentA(t)=(1/2)A_0 andk=-(ln2)(1/5700).
1/2A_0=A_0e^(-(ln2)(1/57000t)
1/2=e^(-(ln2)(1/5700)t) Watershed byA_0.
ln(1/2)=lne^(-(ln2)(1/5700)t) Take logarithms on some sides.
ln(1/2)=-(ln2)/(5700)tlne^x=x
-5700/(ln2)ln(1/2)=t Multiply aside-5700/(ln2)
-5700/(ln2)(ln1-ln2)=t Property (b)
-5700/(ln2)(-ln2)=tln1=0
5700=t
The half life is 5700 years.
(b) Charcoal from an ancient fire pit on Java contained 1/4 the carbon 14 of a living sample of the same sized. Estimate the age of the charcoal.
Let A(t)=1/4A_0 andk=-(ln2)(1/5700).
1/4A_0=A_0e^(-(ln2)(1/5700)t)
1/4=e^(-(ln2)(1/5700)t)
ln(1/4)=lne^(-(ln2)(1/5700)t)
ln(1/4)=(ln2)/(5700)t
-5700/(ln2)ln(1/4)=t
t=11400
The charcoal is around 11400 years old.
Where the Five Star Method to Solve Math Problems Come From
Source: https://quickmath.com/math-tutorials/exponential-and-logarithmic-function.html
0 Response to "Where the Five Star Method to Solve Math Problems Come From"
Post a Comment